多核模糊C均值聚类

摘要：

针对于单一核在处理多数据源和异构数据源方面的不足，多核方法应运而生。本文是将多核方法应用于FCM算法，并对算法做以详细介绍，进而采用MATLAB实现。

在这之前，我们已成功将核方法应用于FCM算法，在很大程度上解决了样本线性不可分的情况。但是这种单一核局限于对数据的某一特征进行有效提取，若一个样本含有多个特征，且遵循不同的核分布，单一核学习就不适用，所以说单一核在处理多数据源以及异构数据源的不足是越发明显。

针对于单一核学习不足，我们可以同时结合多个核函数对数据的多种特征进行同步描述，并且自适应的调整核函数权重对多个核函数进行凸组合，这在一定程度上可以避免了最佳核函数的选择，将这种方法我们称之为多核。

一 多核模糊C均值聚类算法概述

多核方法的本质是用组合后的核函数代替之前的单一核函数。本文主要是将多核方法应用到FCM算法当中，我们暂且将其命名为多核模糊C均值聚类算法（MKFCM），算法的目的是找到最佳的隶属度以及核之间的最优结合方式。MKFC通过将特征的权重嵌入到算法进程中，自动调节权重进行核之间的合并，减轻了无关核对算法的影响，同时充分发挥对学习效果有利核函数对最终聚类结果的作用，反之亦然，这也使得核之间的结合变得合理有效，同时也使得核函数达到最大化利用。接下来对算法进行详细的描述：

1. 目标函数

核方法通过非线性映射将原始数据通过特征映射嵌入到新的特征空间从而发现数据之间的非线性关系。假定在MKFC中，含有M个特征映射，分别记为： ，每一个映射都将原L维数据重新编码为特征空间上的维数为L _k 的向量 。考虑到核方法的应用，可将这些映射分别对应的Mercer核记为 ，根据核的定义则有：

为了使得到的基础核相互结合并且确保构造的的核依旧满足Mercer定理，可假定 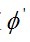为这些特征映射的非负结合，且遵循线性结合：

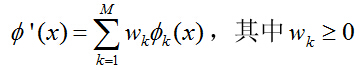
根据之前的分析，核方法是通过特征映射在特征空间上发现数据之间的线性关系，那么采用不同的特征映射重新编码得到数据的维数将不尽相同，上述核之间的线性结合很难实现。因此可根据 ，构造一个新的独立的特征映射集 ，可假定：

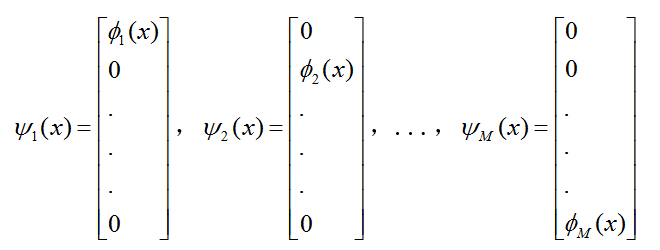
新构造出来的特征映射集的每一个映射分别将原数据X转换为一个L维的向量，其中：

上述分析我们提到，特征空间中数据间的维数不尽相同，考虑到聚类划分依据的是输入空间的数据点，那么可以交互特征间的维数使得数据依旧遵循正交基础。综上分析，新构造的独立特征映射集确保了特征空间上的映射具有相同的维数，因此，采用上述方法进行核之间的线性结合合情合理。同时，这些映射必须遵循一定的正交基础：

其中：

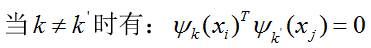
这些正交基础在一定程度上阻止了无关联特征映射之间的交互，同样，这些映射之间存在线性非负关系，因此我们需找到一个关于 的线性非负关系，即找到函数的最优解。那么，对应的目标函数可转化为：                    

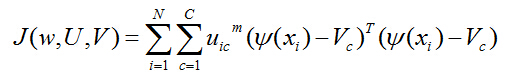
其中：        

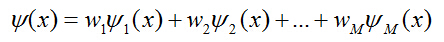
约束条件分别为：

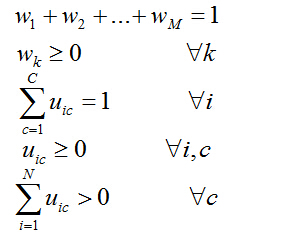
其中， V _c 指的是特征空间上的第c个聚类中心； 代表权重向量；U _ic 是隶属度矩阵U中的元素；V是一个的矩阵，其中矩阵的列分别对应于聚类中心。

  2.  最优化隶属度

MKFC的目的是同时找到目标函数最优化的权重W，隶属度U以及聚类中心V。聚类中心处于不同的特征空间中，直接计算聚类中心是不可能的，但聚类中心是可以用核进行转换的。可以通过给定权重和聚类中心发现最优的隶属度函数，用来表示数据和聚类中心之间的距离：

相应的目标函数为：                                  

该目标函数同样含有约束条件，可引入拉格朗日因子构造新的目标函数：                            

对于隶属度，得到目标函数求极值的最优化条件：                                     

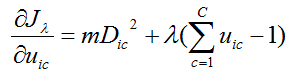
解得：

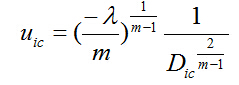
根据约束条件： ，消除拉格朗日因子从而得到闭合解：

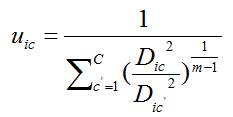
3.  最优化权重

由以上公式可得：权重和聚类中心已知时，可得到最优的隶属度矩阵U。与上述分析方法类似，假定隶属度已知，找寻最优的聚类中心和权重，得到聚类中心关于目标函数求极值的最优化条件：

当U给定时，最优的聚类中心可利用权重加以转换：                  

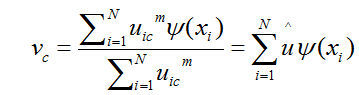
其中 指的是标准化隶属度：

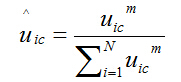
结合之前的讨论，聚类中心处于不同的特征空间，相应的维数不尽相同，比较分析聚类中心是不可能的。据上述公式，聚类中心可以通过转换得到，而在没有聚类中心的情况下可以得到隶属度矩阵和权重的，故只需着力找到最优权重从而得到隶属度矩阵即可，而聚类中心处于闭合解。根据聚类中心的计算公式进行转换：                                                           

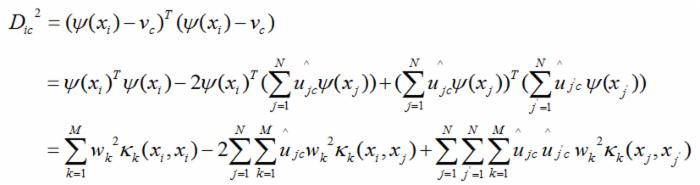
当隶属度函数已知时，即可得出相应的核函数。为了方便计算，可引入系数，将D _ic 转化为：                    

相应的，系数可以表示为：              

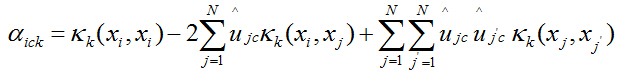
从而目标函数可以转化为：                          

约束条件为：   

当隶属度函数已知时，为了方便计算，引入相应的系数:

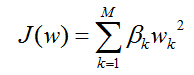
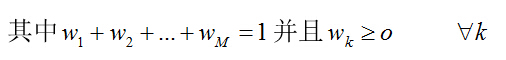
系数为：

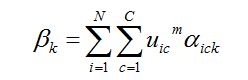
忽略权重非负的约束，引进拉格朗日因子：                          

根据目标函数求极值的最优化条件，有：

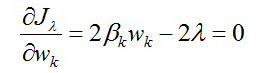
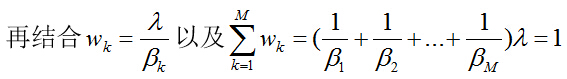
得到：

同时：

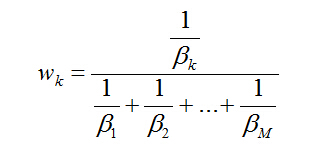
4.   算法步骤

给定一个由N个L维向量组成的数据集、所要分得的类别个数C、自定义一个核函数集、自定义隶属度矩阵以及核权重集。具体的MKFC算法步骤如下：

①初始化隶属度矩阵并满足归一化条件；

②根据公式标准化隶属度；

③根据公式计算系数α；

④根据公式计算系数β；

⑤根据公式更新权重；

⑥根据公式计算距离D _ic ；

⑦根据公式不断更新隶属度；

⑧利用矩阵范数比较迭代的隶属度矩阵，如果 则

停止迭代，否则，返回②。

二  MATLAB实现

在此，我们选取UCI数据库中的数据，结合NMI准则，对算法进行验证和测试，采用MATLAB编程，首先建立MKFCM.m文件，代码如下：

%% 多核模糊C均值聚类 clear all clc; %% load and define load wine.txt data = wine; data(:,1) = []; data_n = size(data,1); M = size(data,2); cluster_n = 3; minr = 0.005;%在计算高斯核时的参数 default_options = [1.08; % 隶属度函数的幂次方   300; % 最大迭代次数   0.0001; %步长   1]; % 判定条件 options = default_options; expo = options(1);  % Exponent for U 隶属度函数的幂次方 max_iter = options(2);  % Max. iteration 最大迭代次数 min_impro = options(3);  % Min. improvement  最小进化步长 display = options(4); Uv = zeros(data_n,cluster_n); membership = zeros(data_n,cluster_n); obj_fcn  = zeros(max_iter,1); K = zeros(M,data_n,data_n); A = zeros(M,data_n,cluster_n); B = zeros(M,1); W = zeros(M,1); D = zeros(data_n,cluster_n); %% 初始化隶属度矩阵并归一 U = rand(data_n,cluster_n);  S = sum(U,2); for i = 1:data_n  for j = 1:cluster_n   U(i,j) = U(i,j) / S(i,1);  end end %% 计算核函数 opeo = zeros(M,1); for i = 1:M  oper = zeros(data_n,data_n);  for j = 1:data_n   for p = 1:data_n   oper(j,p) = (-1 * ((data(j,i) - data(p,i)).^2) / log(minr));   end   end  oprt = reshape(oper,1,data_n * data_n);  oprt(oprt==0) = inf;   opeo(i,1) = min(oprt); end for i = 1:M  for p = 1:data_n   for q = 1:data_n   K(i,p,q) = exp((-1 *(data(p,i) - data(q,i)).^2)/ opeo(i,1));   end  end end %% 开始迭代 for o = 1:max_iter   tic   %% 标准化隶属度矩阵  sum = 0;  for i = 1:data_n   for j = 1:cluster_n    sum = sum + U(i,j).^expo;   end  end  for i = 1:data_n   for j = 1:cluster_n    Uv(i,j) = U(i,j).^expo / sum;   end  end  %% 求参数a    tmp = zeros(M,data_n,cluster_n);  for i = 1:data_n   for c = 1:cluster_n    for k =1:M     for j = 1:data_n      tmp(k,i,c) = tmp(k,i,c) + Uv(j,c) * K(k,i,j);     end    end   end  end  for i = 1:data_n   for c = 1:cluster_n    for k =1:M     tp = 0;     for j = 1:data_n      for q = data_n       tp = tp + Uv(j,c)* Uv(q,c) * K(k,j,q);      end     end     A(k,i,c) = K(k,i,i) - 2 * tmp(k,i,c) + tp;    end   end  end  %% 求系数B  for k = 1:M   for i = data_n    for j = 1:cluster_n       B(k,1) = B(k,1) + U(i,j).^expo * A(k,i,j);    end   end  end  %% 求权重w  sum = 0;  for k = 1:M   sum = sum + B(k,1).^(-1);  end  for k = 1:M   W(k,1) = B(k,1).^(-1) / sum;  end  %% 求欧式距离  for i = 1:data_n   for c = 1:cluster_n    for k = 1:M     D(i,c) = D(i,c) + A(k,i,c) * W(k,1).^2;    end   end  end  %% 更新隶属度矩阵  for i = 1:data_n   for c = 1:cluster_n    sum = 0;    for q = 1:cluster_n     sum = sum + (D(i,c) / D(i,q)).^(1 / (expo - 1));    end    membership(i,c) = 1 / sum;   end  end  sum = zeros(data_n,1);  for i =1:data_n   for j = 1:cluster_n    sum(i,1) = sum(i,1) + membership(i,j);   end  end  for i = 1:data   for j = 1:cluster_n    membership(i,j) = membership(i,j) / sum(i,1);   end  end   %% 得到目标函数  temp = 0;  for i = 1:data_n   for c = 1:cluster_n    temp = temp + membership(i,c).^expo;    trmp = 0;    for k = 1:M     trmp = trmp + A(k,i,c) * W(k,1).^2 ;    end   end  end  obj_fcn(o) = temp * trmp;  if display,   fprintf('Iteration count = %d, obj_fcn = %f/n', o, obj_fcn(o));  end  if o > 1   if max(abs(membership - U)) < min_impro;    break   else    U  = membership;   end  end  toc end %% 计算NMI值 B = ones(data_n,1); for i = 1:data_n  for j = 1:cluster_n   if membership(i,B(i,1)) < membership(i,j)    B(i,1) = j;   end  end end B = reshape(B,1,data_n); A = wine(:,1); A = reshape(A,1,data_n); t = nmi(A,B); %% 输出 plot(membership(:,1),'-ro'); grid on hold on plot(membership(:,2),'-g*'); plot(membership(:,3),'-b+'); ylabel('Membership degrees') legend('MKFC1','MKFC2','MKFC3','location','northeast'); 

接下来采用NMI准则对算法进行评估，NMI用来评价聚类结果的相似程度，求出MI的值，进而用熵做分母，对MI值进行标准化。可以采用NMI将各个算法的聚类结果与标准结果进行比较，值越接近1，表明聚类效果越好；若值趋近于０，则表明聚类效果很差，采用MATLAB编程代码如下：

function [NMI] = nmi(A,B) total = size(A,2); A_i = unique(A); A_c = length(A_i); B_i = unique(B); B_c = length(B_i); idA = double (repmat(A,A_c,1) == repmat(A_i',1,total)); idB = double (repmat(B,B_c,1) == repmat(A_i',1,total)); idAB = idA * idB';  Sa = zeros(A_c,1); Sb = zeros(B_c,1); for i = 1:A_c   for j = 1:total   if idA(i,j) == 1    Sa(i,1) = Sa(i,1) + 1;   end  end end for i = 1:B_c  for j = 1:total   if idB(i,j) ==1    Sb(i,1) = Sb(i,1) + 1;   end  end end Pa = zeros(A_c,1); Pb = zeros(B_c,1); for i = 1:A_c  Pa(i,1) = Sa(i,1) / total; end for i = 1:B_c  Pb(i,1) = Sa(i,1) / total; end Pab = idAB / total; Ha = 0; Hb = 0; for i = 1:A_c  Ha = Ha + Pa(i,1) * log2(Pa(i,1)); end for i = 1:B_c  Hb = Hb + Pb(i,1) * log2(Pb(i,1)); end MI = 0; for i = 1:A_c  for j = 1:B_c    MI = MI + Pab(i,j) * log2(Pab(i,j) / (Pa(i,1) * Pb(j,1)) + eps);  end end NMI = MI / ((Ha * Hb).^(1/2)); fprintf('NMI = %d/n',NMI); 

选取UCI库中的多种数据，分别计算NMI值和之前的算法比较，可以得到MKFCM的优越性，大家可以自行检验。

以上是个人的一些理解与总结，也难免有错，望不吝赐教！