转载

连续变量的朴素贝叶斯 | AlgorithmDog

朴素贝叶斯算法是一种常用而有效的分类算法。朴素贝叶斯算法一般处理离散型的属性变量。但是很多情况下，我们会碰到连续型的属性变量。那么朴素贝叶斯算法如何处理连续型的属性变量呢？ /(/)

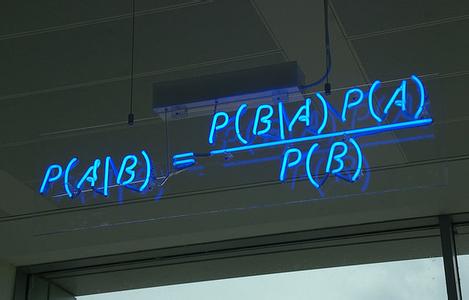
1. 朴素贝叶斯

朴素贝叶斯分应用了贝叶斯定理。对于一个实例 /(/pmb{x}=(x_1,x_2,x_3,...,x_d)/)

$/pmb{x}=(x_1,x_2,x_3,...,x_d)$ ，其属于某个类别 /(c/) $c$ 的后验概率
/begin{eqnarray}
p(c|x_1,...,x_d) = /frac{p(p(x_1,...,x_d)|c)p(c)}{p(x_1,...,x_d)} /nonumber
/end{eqnarray}
朴素贝叶斯假设属性变量相互独立。这时后验概率
/begin{eqnarray}
p(c_1|x_1,...,x_d) = /frac{p(p(x_1|c_1),...,p(x_d|c_1)p(c_1)} {/sum_{c}p(p(x_1|c),...,p(x_d|c)p(c)} /nonumber
/end{eqnarray}

在预测阶段，朴素贝叶斯选择后验概率最大的类别作为预测结果。
/begin{eqnarray}
/hat{c} = argmax_{c}p(c|x_1,...,x_d) /nonumber
/end{eqnarray}

在训练阶段，朴素贝叶斯算法需要计算 /(p(c)/)

2. 处理连续属性变量

如果属性变量是连续变量，在训练阶段我们要估计的依然是某个类别下属性变量的概率 /(p(x_i|c)/)

$p(x_i|c)$ 。只是这个时候，属性变量 /(x_i/) $x_i$ 是一个连续变量。我们常用下面两种方法处理。

2.1. 利用高斯分布

这种方法假设 /(p(x_i|c/)

$p(x_i|c$ 服从高斯分布 /(N(u_i,/sigma_i)/) $N(u_i,/sigma_i)$ 。遍历训练数据计算出类别 /(c/) $c$ 下属性变量 /(x_i/) $x_i$ 的样本均值 /(/hat{u}_i/) $/hat{u}_i$ 和样本方差 /(/hat{/sigma}_i/) $/hat{/sigma}_i$ 。让 /(u_i = /hat{u}_i/) $u_i = /hat{u}_i$ 和 /(/sigma_i = /hat{/sigma}_i/) $/sigma_i = /hat{/sigma}_i$ ，就完成了训练。

这种方法的进阶是使用多个高斯分布，即假设 /(p(x_i|c/)

$p(x_i|c$ 服从分布 /(N(u_{i,1},/sigma_{i,1})/) $N(u_{i,1},/sigma_{i,1})$ + ... + /(N(u_{i,k},/sigma_{i,k})/) $N(u_{i,k},/sigma_{i,k})$ 。本质上这种进阶方法利用高斯混合模型 (Gauss Mixed Model, GMM) 估计 /(p(x_i|c)/) $p(x_i|c)$ 。高斯混合模型最常见的求解方法是 EM 算法，详情可参见文章

2.2. 核密度估计

接下来，我们重点介绍核密度估计 (Kernel Density Estimates，KDE)。核密度估计是在概率论中用来估计未知的密度函数，属于非参数检验方法之一，由Rosenblatt (1955)和Emanuel Parzen(1962)提出，又名Parzen窗（Parzen window）。

如果在某个类别下属性变量 /(x_i/)

$x_i$ 的第 /(j/) $j$ 个观测值是 /(s_{i,j}/) $s_{i,j}$ ，我们认为属性变量 /(x_i/) $x_i$ 在这个数 /(s_{i,j}/) $s_{i,j}$ 附近的概率密度会比较大，而在这个数远处概率密度会比较小。基于这种想法，针对观察中的属性变量的每一个值 /(s_{i,j}/) $s_{i,j}$ ，我们都用 /(f(x_i-s_{i,j})/) $f(x_i-s_{i,j})$ 去拟合这个远小近大概率密度。其中 /(x_i-s_{i,j}/) $x_i-s_{i,j}$ 越靠近零， /(f(x_i-s_{i,j})/) $f(x_i-s_{i,j})$ 越大；反之反是。

/begin{eqnarray}
p(x_i|c) = /frac{1}{N} /sum_{j=1}^N f_j(x_i-s_{i,j}) /nonumber
/end{eqnarray}

/(f(x_i-s_{i,j})/)

$f(x_i-s_{i,j})$ 便是核密度估计的核函数。常有核函数是下面三种。

矩阵核
/begin{eqnarray}
f_j(x_i-s_{i,j}) = /left/{/begin{matrix}
/frac{1}{2} & |x_i - s_{i,j}| /le 1//
0 & otherwise /nonumber
/end{matrix}/right.
/end{eqnarray}

Epanechnikov 核

/begin{eqnarray}
f_j(x_i-s_{i,j}) = /left/{/begin{matrix}
/frac{4}{3}/{1-(x_i - s_{i,j})^2/} & |x_i - s_{i,j}| /le 1//
0 & otherwise /nonumber
/end{matrix}/right.
/end{eqnarray}

高斯核

/begin{eqnarray}
f_j(x_i-s_{i,j}) = N(x_i - s_{i,j}, z^2) /nonumber
/end{eqnarray}