转载

计算机中的进制&位运算

在十进制中，个位的1代表10⁰=1，十位的1代表10¹=10，百位的1代表10²=100，所以：123=1×10²+2×10¹+3×10⁰

同样道理，在二进制中，个位的1代表2⁰=1，十位的1代表2¹=2，百位的1代表2²=4，所以:(A3A2A1A0)₂=A3×2³+A2×2²+A1×2¹+A0×2⁰

如果二进制和十进制数出现在同一个等式中，为了区别我们用(A3A2A1A0)₂这种形式表示A3A2A1A0是二进制数，每个数字只能是0或1，其它没有套括号加下标的数仍表示十进制数。对于(A3A2A1A0)₂这样一个二进制数，最左边的A3位称为最高位（MSB，Most Significant Bit），最右边的A0位称为最低位（LSB，Least Significant Bit）。以后我们遵循这样的惯例： LSB称为第0位而不是第1位，所以如果一个数是32位的，则MSB是第31位。上式就是从二进制到十进制的换算公式。

下面来看十进制怎么换算成二进制。我们知道

13=1×2³+1×2²+0×2¹+1×2⁰ 所以13换算成二进制应该是(1101)₂。问题是怎么把13分解成等号右边的形式呢？注意到等号右边可以写成

13=(((0×2+1₃)×2+1₂)×2+0₁)×2+1₀

我们将13反复除以2取余数就可以提取出上式中的1101四个数字，为了让读者更容易看清楚是哪个1和哪个0，上式和下式中对应的数字都加了下标：

13÷2=6...1₀ 6÷2=3...0₁ 3÷2=1...1₂ 1÷2=0...1₃

把这四步得到的余数按相反的顺序排列就是13的二进制表示，因此这种方法称为除二反序取余法。

计算机用二进制表示数，程序员也必须习惯使用二进制，但二进制写起来太啰嗦了，所以通常将二进制数分成每三位一组或者每四位一组，每组用一个数字表示。比如把(10110010)₂从最低位开始每三位分成一组，10、110、010，然后把每组写成一个十进制数字，就是(262)₈，这样每一位数字的取值范围是0~7，逢八进一，称为八进制（Octal）。类似地，把(10110010)₂分成每四位一组，1011、0010，然后把每组写成一个数字，这个数的低位是2，高位已经大于9了，我们规定用字母A~F表示10~15，这个数可以写成(B2)₁₆，每一位数字的取值范围是0~F，逢十六进一，称为十六进制（Hexadecimal）。所以，八进制和十六进制是程序员为了书写二进制方便而发明的简便写法，好比草书和正楷的关系一样。

位运算：

整数在计算机中用二进制的位来表示，C语言提供一些运算符可以直接操作整数中的位，称为位运算。

1.1. 按位与、或、异或、取反运算

按位与(&)：两个操作数都是1，结果是1，否则是0
或(|)：两个操作数有一个1，结果是1
异或(^)：两个操作数相同则结果为0，两个操作数不同则结果为1
取反运算(~)：对操作数取反

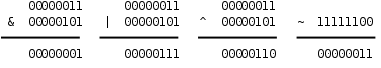
1.2. 移位运算

移位运算符（Bitwise Shift）包括左移<<和右移>>。左移将一个整数的各二进制位全部左移若干位，例如0xcfffffff3<<2得到0x3fffffcc：

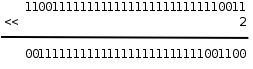
Java 平台都是有符号整数，所以上述图一操作在Java中符号位发生了变化值由（-805306381）变为（1073741772）

在一定的取值范围内，将一个整数左移1位相当于乘以2。比如二进制11（十进制3）左移一位变成110，就是6，再左移一位变成1100，就是12。读者可以自己验证这条规律对有符号数和无符号数都成立，对负数也成立。当然，如果左移改变了最高位（符号位），那么结果肯定不是乘以2了，所以我加了个前提“ 在一定的取值范围内 ”。由于计算机做移位比做乘法快得多，编译器可以利用这一点做优化，比如看到源代码中有i * 8，可以编译成移位指令而不是乘法指令。

当操作数是无符号数时，右移运算的规则和左移类似，例如0xcffffff3>>2得到0x33fffffc：

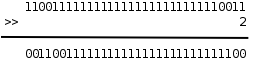
Java 平台执行结果：值由-805306381 变成 -201326596 仍然保留负数的符号位，相当于除以4

最低两位的11被移出去了，最高两位又补了两个0，其它位依次右移两位。和左移类似，移动的位数也必须小于左操作数的总位数，否则结果是Undefined。在一定的取值范围内，将一个整数右移1位相当于除以2，小数部分截掉。

当操作数是有符号数时，右移运算的规则比较复杂：

如果是正数，那么高位移入0
如果是负数，那么高位移入1还是0不一定，这是Implementation-defined的。对于x86平台的gcc编译器，最高位移入1，也就是仍保持负数的符号位，这种处理方式对负数仍然保持了“右移1位相当于除以2”的性质。

综上所述，由于类型转换和移位等问题，用有符号数做位运算是很不方便的，所以， 建议只对无符号数做位运算，以减少出错的可能 。

1.3. 掩码：

如果要对一个整数中的某些位进行操作，怎样表示这些位在整数中的位置呢？可以用掩码（Mask）来表示。比如掩码 0x0000ff00 表示对一个32位整数的8~15位进行操作，举例如下。

1、取出8~15位。

unsigned int a, b, mask = 0x0000ff00;
a = 0x12345678;
b = (a & mask) >> 8; /* 0x00000056 */
复制代码

2、将8~15位清0。

unsigned int a, b, mask = 0x0000ff00;
a = 0x12345678;
b = a & ~mask; /* 0x12340078 */
复制代码

3、将8~15位置1。

unsigned int a, b, mask = 0x0000ff00;
a = 0x12345678;
b = a | mask; /* 0x1234ff78 */
复制代码

位运算在雪花算法的应用：

12bits 毫秒增量的最大值：1右移12位减去1,可以自己用等比数列计算下12bit的最大值，看是否和位移的结果一致;二进制表示：（...001111 1111 1111）(14位以后的0用省略号代替)
10bits 工作进程Id ：1右移10位，这里我有个疑问,不应该再减去1,才是最大值么
判断是否需要获取下一个时间的依据： 0L == (sequence = ++sequence & SEQUENCE_MASK) sequence和最大值两个数 按位与 ，只有当sequence大于SEQUENCE_MASK 的时候，&的结果是0，获取下一个时间戳
41bits：(currentMillis - EPOCH) << TIMESTAMP_LEFT_SHIFT_BITS，通过右移22位，空出10bits的进程ID位、12bits的毫秒自增量
((currentMillis - EPOCH) << TIMESTAMP_LEFT_SHIFT_BITS) | (workerId << WORKER_ID_LEFT_SHIFT_BITS) | sequence; 41bits|10bits|12bits，因为右移低位补0，按位或操作，其实就是操作数本身。

shrding-jdbc默认的实现：

/**
 * 默认的主键生成器.
 * 
 * <p>
 * 长度为64bit,从高位到低位依次为
 * </p>
 * 
 * <pre>
 * 1bit   符号位 
 * 41bits 时间偏移量从2016年11月1日零点到现在的毫秒数
 * 10bits 工作进程Id
 * 12bits 同一个毫秒内的自增量
 * </pre>
 * 
 * <p>
 * 工作进程Id获取优先级: 系统变量{@code sharding-jdbc.default.key.generator.worker.id} 大于 环境变量{@code SHARDING_JDBC_DEFAULT_KEY_GENERATOR_WORKER_ID}
 * ,另外可以调用@{@code DefaultKeyGenerator.setWorkerId}进行设置
 * </p>
 * 
 * @author gaohongtao
 */
@Getter
@Slf4j
public final class DefaultKeyGenerator implements KeyGenerator {
    
    public static final long EPOCH;
    
    public static final String WORKER_ID_PROPERTY_KEY = "sharding-jdbc.default.key.generator.worker.id";
    
    public static final String WORKER_ID_ENV_KEY = "SHARDING_JDBC_DEFAULT_KEY_GENERATOR_WORKER_ID";
    
    private static final long SEQUENCE_BITS = 12L;
    
    private static final long WORKER_ID_BITS = 10L;
    
    private static final long SEQUENCE_MASK = (1 << SEQUENCE_BITS) - 1;
    
    private static final long WORKER_ID_LEFT_SHIFT_BITS = SEQUENCE_BITS;
    
    private static final long TIMESTAMP_LEFT_SHIFT_BITS = WORKER_ID_LEFT_SHIFT_BITS + WORKER_ID_BITS;
    
    private static final long WORKER_ID_MAX_VALUE = 1L << WORKER_ID_BITS;
    
    @Setter
    private static TimeService timeService = new TimeService();
    
    @Getter
    private static long workerId;
    
    static {
        Calendar calendar = Calendar.getInstance();
        calendar.set(2016, Calendar.NOVEMBER, 1);
        calendar.set(Calendar.HOUR_OF_DAY, 0);
        calendar.set(Calendar.MINUTE, 0);
        calendar.set(Calendar.SECOND, 0);
        calendar.set(Calendar.MILLISECOND, 0);
        EPOCH = calendar.getTimeInMillis();
        initWorkerId();
    }
    
    private long sequence;
    
    private long lastTime;
    
    public static void initWorkerId() {
        String workerId = System.getProperty(WORKER_ID_PROPERTY_KEY);
        if (!Strings.isNullOrEmpty(workerId)) {
            setWorkerId(Long.valueOf(workerId));
            return;
        }
        workerId = System.getenv(WORKER_ID_ENV_KEY);
        if (Strings.isNullOrEmpty(workerId)) {
            return;
        }
        setWorkerId(Long.valueOf(workerId));
    }
    
    /**
     * 设置工作进程Id.
     * 
     * @param workerId 工作进程Id
     */
    public static void setWorkerId(final long workerId) {
        Preconditions.checkArgument(workerId >= 0L && workerId < WORKER_ID_MAX_VALUE);
        DefaultKeyGenerator.workerId = workerId;
    }
    
    /**
     * 生成Id.
     * 
     * @return 返回@{@link Long}类型的Id
     */
    @Override
    public synchronized Number generateKey() {
        long currentMillis = timeService.getCurrentMillis();
        Preconditions.checkState(lastTime <= currentMillis, "Clock is moving backwards, last time is %d milliseconds, current time is %d milliseconds", lastTime, currentMillis);
        if (lastTime == currentMillis) {
            if (0L == (sequence = ++sequence & SEQUENCE_MASK)) {
                currentMillis = waitUntilNextTime(currentMillis);
            }
        } else {
            sequence = 0;
        }
        lastTime = currentMillis;
        if (log.isDebugEnabled()) {
            log.debug("{}-{}-{}", new SimpleDateFormat("yyyy-MM-dd HH:mm:ss.SSS").format(new Date(lastTime)), workerId, sequence);
        }
        return ((currentMillis - EPOCH) << TIMESTAMP_LEFT_SHIFT_BITS) | (workerId << WORKER_ID_LEFT_SHIFT_BITS) | sequence;
    }
    
    private long waitUntilNextTime(final long lastTime) {
        long time = timeService.getCurrentMillis();
        while (time <= lastTime) {
            time = timeService.getCurrentMillis();
        }
        return time;
    }
}
复制代码

原文 https://juejin.im/post/5c0296aae51d454556295dc5

正文到此结束