Codeforces Round#323
City X consists of n vertical and n horizontal infinite roads, forming n × n intersections. Roads (both vertical and horizontal) are numbered from 1 to n , and the intersections are indicated by the numbers of the roads that form them.
Sand roads have long been recognized out of date, so the decision was made to asphalt them. To do this, a team of workers was hired and a schedule of work was made, according to which the intersections should be asphalted.
Road repairs are planned for n 2 days. On the i -th day of the team arrives at the i -th intersection in the list and if none of the two roads that form the intersection were already asphalted they asphalt both roads. Otherwise, the team leaves the intersection, without doing anything with the roads.
According to the schedule of road works tell in which days at least one road will be asphalted.
The first line contains integer n ( 1 ≤ n ≤ 50 ) — the number of vertical and horizontal roads in the city.
Next n 2 lines contain the order of intersections in the schedule. The i -th of them contains two numbers h i , v i ( 1 ≤ h i , v i ≤ n ), separated by a space, and meaning that the intersection that goes i -th in the timetable is at the intersection of the h i -th horizontal and v i -th vertical roads. It is guaranteed that all the intersections in the timetable are distinct.
In the single line print the numbers of the days when road works will be in progress in ascending order. The days are numbered starting from 1 .
C++
2 1 1 1 2 2 1 2 2
C++
| 1 4 |
C++
1 1 1
C++
| 1 |
题解:阅读题,当修一个节点时,就会同时把该节点的横街道和竖街道都修了,问,按照题目中给的计划,最后真正修的节点是哪些。
C++
#include<iostream> using namespace std; int n,i,A[51],B[51],h,v; int main() { cin>>n; for(i=1; i<=n*n; i++) { cin>>h>>v; if(A[h]==0 && B[v]==0) { cout<<i<<" "; A[h]=B[v]=1; } } return 0; } B. Robot’s Task
Robot Doc is located in the hall, with n computers stand in a line, numbered from left to right from 1 to n . Each computer contains exactly one piece of information, each of which Doc wants to get eventually. The computers are equipped with a security system, so to crack the i -th of them, the robot needs to collect at least a i any pieces of information from the other computers. Doc can hack the computer only if he is right next to it.
The robot is assembled using modern technologies and can move along the line of computers in either of the two possible directions, but the change of direction requires a large amount of resources from Doc. Tell the minimum number of changes of direction, which the robot will have to make to collect all n parts of information if initially it is next to computer with number 1 .
It is guaranteed that there exists at least one sequence of the robot’s actions, which leads to the collection of all information. Initially Doc doesn’t have any pieces of information.
The first line contains number n ( 1 ≤ n ≤ 1000 ). The second line contains n non-negative integers a 1 , a 2 , …, a n ( 0 ≤ a i < n ), separated by a space. It is guaranteed that there exists a way for robot to collect all pieces of the information.
Print a single number — the minimum number of changes in direction that the robot will have to make in order to collect all n parts of information.
C++
3 0 2 0
C++
| 1 |
C++
5 4 2 3 0 1
C++
| 3 |
C++
7 0 3 1 0 5 2 6
C++
| 2 |
题解:我靠啊,这是考英语还是考算法啊,再各种题解的帮助下花了半个小时把题目终于读懂了,就是每次只能取大于它的最小的数,问要变化多少次方向才能取完所有的数。暴力即可
C++
#include <bits/stdc++.h> using namespace std; int n,a[1001],ans,cur,v[1001]; int main(){ cin>>n; for(int i=0;i<n;++i) cin>>a[i]; int di=1; for(int i=0;cur<n;i+=di){ if(i==n) { di=-1; ++ans; } else if(i==-1) { di=1; ++ans; } else if(a[i]<=cur&&!v[i]){ v[i]=1; ++cur; } } cout<<ans<<endl; } C. GCD Table
The GCD table G of size n × n for an array of positive integers a of length n is defined by formula

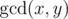 . For example, for array a = {4, 3, 6, 2} of length 4 the GCD table will look as follows:
. For example, for array a = {4, 3, 6, 2} of length 4 the GCD table will look as follows:
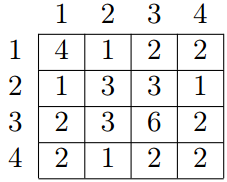
The first line contains number n ( 1 ≤ n ≤ 500 ) — the length of array a . The second line contains n 2 space-separated numbers — the elements of the GCD table of G for array a .
All the numbers in the table are positive integers, not exceeding 10 9 . Note that the elements are given in an arbitrary order. It is guaranteed that the set of the input data corresponds to some array a .
In the single line print n positive integers — the elements of array a . If there are multiple possible solutions, you are allowed to print any of them.
C++
4 2 1 2 3 4 3 2 6 1 1 2 2 1 2 3 2
C++
C++
1 42
| 1 42 |
C++
| 42 |
C++
2 1 1 1 1
C++
| 1 1 |
题解:最大的数肯定是数组中的一个数,然后从后往前贪心就对啦。
C++
#include <iostream> #include <algorithm> #include <set> using namespace std; typedef long long ll; const int maxn = 500 + 7; multiset <int> ms; int arr[maxn]; int main() { ios::sync_with_stdio(0); cin.tie(0); int n; cin >> n; for (int i = 0; i < n * n; ++i) { int x; cin >> x; ms.insert(x); } for (int i = n - 1; i >= 0; --i) { arr[i] = *ms.rbegin(); ms.erase(ms.lower_bound(arr[i])); for (int j = i + 1; j < n; ++j) { int gcdi = __gcd(arr[i], arr[j]); ms.erase(ms.lower_bound(gcdi)); ms.erase(ms.lower_bound(gcdi)); } } for (int i = 0; i < n; ++i) cout << arr[i] << " "; cout << "/n"; return 0; } 










![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)

