高精度加、减、乘、除算法实现详解

在说高精度加减乘除运算之前，我们先搞明白什么是高精度运算？

实际上高精度就是说参与运算的数据和运算结果的范围，超出标准数据类型能表示的数据大小范围的运算。这个时候，如果要得到正确的计算结果，显然不能依靠普通方法实现了。而要在普通运算原理的基础上，加以辅助算法来实现超大数据的计算。例如：求两个100位的数据的和，或者计算两个100位的数字乘积。这时就要用到高精度算法了。

一、高精度加法：

高精度加法的实现原理：

1、计算结果的位数

358934760892734899共18位

38960302975237462共17位

故结果不会超过19位。

2、将要计算的数字分割成多段，按照顺序排列（这里以0-32767作为每一存储单位存储的数的限制）：

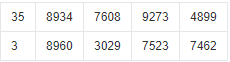
（为提高空间利用效率，可以一个存储单位存储多位数。）

3、将两数相加。

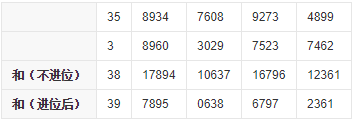
4、输出结果。

从高位到低位依次输出。除最高位以外，其他低位上不足4位的要在前面补上0。

5.代码实现如下

#include<iostream>  
#include<cstring>  
using namespace std;  
int main()  
{  
  string str1,str2;  
  int a[250],b[250],len;   //数组的大小决定了计算的高精度最大位数  
  int i;  
  memset(a,0,sizeof(a));  
  memset(b,0,sizeof(b));  
  cin>>str1>>str2;   //输入两个字符串  
  a[0]=str1.length();  //取得第一个字符串的长度  
  for(i=1;i<=a[0];i++)  //把第一个字符串转换为整数，存放在数组a中  
    a[i]=str1[a[0]-i]-'0';  
  b[0]=str2.length();   //取得第二个字符串长度  
  for(i=1;i<=b[0];i++)   //把第二个字符串中的每一位转换为整数，存放在数组B中  
    b[i]=str2[b[0]-i]-'0';  
  len=(a[0]>b[0]?a[0]:b[0]);   //取两个字符串最大的长度  
  for(i=1;i<=len;i++)   //做按位加法，同时处理进位  
  {  
    a[i]+=b[i];  
    a[i+1]+=a[i]/10;  
    a[i]%=10;     
  }  
  len++;    //下面是去掉最高位的0，然后输出。  
  while((a[len]==0)&&(len>1)) len--;  
  for(i=len;i>=1;i--)  
    cout<<a[i];  
  return 0;   
}  
   
//注意：两个数相加，结果的位数，应该比两个数中大的那个数多一位。

二、高精度减法：

高精度减法的实现原理：

1.高精度减法相比高精度加法来说，稍微复杂一点，因为减法在差为负数时处理的细节更多一点：当被减数小于减数时，差为负数，差的绝对值是减数减去被减数；在程序实现上用一个变量来存储符号位，用另一个数组存差的绝对值。

2.实现流程

(1).先比较大小

(2).决定输出符号，为正还是为负

(3).按位减法，并注意处理借位

3.代码实现如下：

#include<iostream>  
using namespace std;  
int compare(string s1,string s2);  
int main()  
{  
  string str1,str2;  
  int a[250],b[250],len;  
  int i;  
  memset(a,0,sizeof(a));  
  memset(b,0,sizeof(b));  
  cin>>str1>>str2;  
  a[0]=str1.length();  
  for(i=1;i<=a[0];i++)  
    a[i]=str1[a[0]-i]-'0';  
  b[0]=str2.length();  
  for(i=1;i<=b[0];i++)  
    b[i]=str2[b[0]-i]-'0';  
  if((compare(str1,str2))==0)  //大于等于，做按位减，并处理借位。  
  {  
    for(i=1;i<=a[0];i++)  
      {a[i]-=b[i];  
       if (a[i]<0) {a[i+1]--;a[i]+=10;}  
      }  
    a[0]++;  
    while((a[a[0]]==0)&&(a[0]>1)) a[0]--;  
    for(i=a[0];i>=1;i--)  
      cout<<a[i];  
    cout<<endl;   
  }                            
  else  
  {  
    cout<<'-';  //小于就输出负号  
    for(i=1;i<=b[0];i++)  //做按位减，大的减小的  
      {b[i]-=a[i];  
       if (b[i]<0) {b[i+1]--;b[i]+=10;}  
      }  
    b[0]++;  
    while((b[b[0]]==0)&&(b[0]>1)) b[0]--;  
    for(i=b[0];i>=1;i--)  
      cout<<b[i];  
    cout<<endl;          
  }  
  return 0;   
}  
int compare(string s1,string s2)  //比较字符串（两个数）数字的大小，大于等于返回0，小于返回1。  
{  
  if(s1.length()>s2.length()) return 0;  //先比较长度，哪个字符串长，对应的那个数就大  
  if(s1.length()<s2.length()) return 1;  
  for(int i=0;i<=s1.length();i++)  //长度相同时，就一位一位比较。  
  {  
    if(s1[i]>s2[i]) return 0;  
    if(s1[i]<s2[i]) return 1;                            
  }  
  return 0;   //如果长度相同，每一位也一样，就返回0，说明相等  
}

三、高精度乘法实现

高精度乘法实现原理：

1.由于数字较大，无法使用简单的数据结构进行存储，选用数组和字符串来存储数字，字符串方便我们对于高位整数的输入，而整形数组的简便有利于每个位数的计算，结合两者优点便可实现高精度乘法。

2.实现过程：

(1).通过两个字符串输入两个整数

(2).引入两个数组，将每个整数切割存储到数组里面

(3).进行每一位的运算

(4).处理进位

(5).输出结果

3.代码实现如下：

#include<iostream>  
#include<cstring>  
using namespace std;  
int main()  
{  
  string str1,str2;  
  int a[250],b[250],c[500],len;    //250位以内的两个数相乘  
  int i,j;  
  memset(a,0,sizeof(a));  
  memset(b,0,sizeof(b));  
  cin>>str1>>str2;  
  a[0]=str1.length();  
  for(i=1;i<=a[0];i++)  
    a[i]=str1[a[0]-i]-'0';  
  b[0]=str2.length();  
  for(i=1;i<=b[0];i++)  
    b[i]=str2[b[0]-i]-'0';  
  memset(c,0,sizeof(c));  
  for(i=1;i<=a[0];i++)   //做按位乘法同时处理进位，注意循环内语句的写法。  
    for(j=1;j<=b[0];j++)  
    {  
    c[i+j-1]+=a[i]*b[j];  
    c[i+j]+=c[i+j-1]/10;  
    c[i+j-1]%=10;     
    }  
  len=a[0]+b[0]+1;  //去掉最高位的0，然后输出  
  while((c[len]==0)&&(len>1)) len--;   //为什么此处要len>1??  
  for(i=len;i>=1;i--)  
    cout<<c[i];  
  return 0;   
}

四、高精度除法实现

高精度除法实现原理：高精度除法这一块比较复杂，它可以分为两种情况：

第一种情况：高精除以低精，实际上就是对被除的每一位，包括前面的余数都除以除数。

代码实现如下：

#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
int main()
{
    char a1[100],c1[100];
    int a[100],c[100],lena,i,x=0,lenc,b;
    memset(a,0,sizeof(a));
    memset(c,0,sizeof(c));
    gets(a1);  //输入高精度被除数 
    cin>>b;    //输入低精度除数 
    lena=strlen(a1);
    for (i=0;i<=lena-1;i++)
　　      a[i+1]=a1[i]-48;   //将高精度被除数放入a数组 
    for (i=1;i<=lena;i++)            //按位相除
        {
            c[i]=(x*10+a[i])/b;
                x=(x*10+a[i])%b;
        }
　   lenc=1;
    while (c[lenc]==0&&lenc<lena) 
 　  lenc++;       //删除前导0
    for (i=lenc;i<=lena;i++) 
    cout<<c[i];
    cout<<endl;
    return 0;
}

第二种情况：高精除以高精

代码实现如下：

#include<iostream>
#include<cstring>
using namespace std;
int a[100],b[100],c[100];
int compare(int a[],int b[])//比较a、b，若a>b为1；若a<b为-1；若a=b为0
{
    int i;
    if(a[0]>b[0])
        return 1;
    if(a[0]<b[0])
        return -1;
    for(i=a[0];i>0;i--)//从高位到低位比较
    {
        if(a[i]>b[i])
            return 1;
        if(a[i]<b[i])
            return -1;
    }
    return 0;
}

void subduction(int a[],int b[])//计算a=a-b
{
    int flag;
    int i;

    flag=compare(a,b);
    if(flag==0)//相等
    {
        a[0]=0;
        return;
    }
    if(flag==1)//大于
    {
        for(i=1;i<=a[0];i++)
        {
            if(a[i]<b[i])//若不够向上借位
            {
                a[i+1]--;
                a[i]+=10;
            }
            a[i]-=b[i];
        }
        while(a[0]>0&&a[a[0]]==0)//删除前导0
            a[0]--;
        return;
    }
}
int main()
{
    char str1[100],str2[100];
    int i,j;

    memset(a,0,sizeof(a));
    memset(b,0,sizeof(b));
    memset(c,0,sizeof(c));

    cin>>str1>>str2;
    a[0]=strlen(str1);//a[0]存储串1的位数
    b[0]=strlen(str2);//b[0]存储串2的位数
    for(i=1;i<=a[0];i++)
        a[i]=str1[a[0]-i]-'0';
    for(i=1;i<=b[0];i++)
        b[i]=str2[b[0]-i]-'0';


    int temp[100];
    c[0]=a[0]-b[0]+1;
    for(i=c[0];i>0;i--)
    {
        memset(temp,0,sizeof(temp));

        for(j=1;j<=b[0];j++)//从i开始的地方，复制数组b到数组temp
            temp[j+i-1]=b[j];
        temp[0]=b[0]+i-1;

        while(compare(a,temp)>=0)//用减法模拟
        {
            c[i]++;
            subduction(a,temp);
        }
    }

    while(c[0]>0&&c[c[0]]==0)//删除前导0
        c[0]--;

    cout<<"商为：";
    if(c[0]==0)//输出结果
        cout<<0<<endl;
    else
    {
        for(i=c[0];i>0;i--)
            cout<<c[i];
        cout<<endl;
    }

    cout<<"余数为：";
    if(a[0]==0)//输出余数
        cout<<0<<endl;
    else
    {
        for(i=a[0];i>0;i--)
            cout<<a[i];
        cout<<endl;
    }

    return 0;
}