随机化算法与素性测试

大家好，这是上班以后的第一篇blog，预计后边算法还有2篇。也就是说这是本人算法系列倒数第3篇，感谢大家的指正，今天是说明随机化算法。

随机数发生器

真正的随机性在计算机上，是不可能的！因为这些数的生成依赖于算法，从而不可能是随机的。所以计算机产生的都是 伪随机数

基本理论

生产随机数的最简单办法是 线性同余数发生器 。

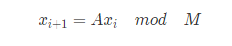
从上面的公式可知：

1. 为了开始这个序列必须给出x0（ x0叫做种子 ）。如果x0=0,那么这个序列绝不会是随机的。
2. M为素数，则xi绝不会是0.

如果A和M选择的正确，那么1<=x0< M 都是等概率出现的。

举例说明A和M选值的重要性

1. M=11，A=7，x0=1，所生成的随机数为： 7 ,5,2,3,10,4,6,9,8,1, 7 ，… 在M-1=10后，该序列将重复。 所以M必须为非常大的素数
2. A的选择也将影响随机性 ，例如A=5，M=11，x0=1 将有一个短周期： 5,3,4,9,1,5，…

Java中实现

在Java中使用修改后的48比特线性同余数发生器, 并只返回高32位 。以防止低阶bit位上循环的问题。

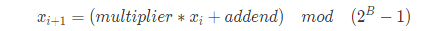
其中: multiplier=25214903917,B=48,addend=11 而x0采用 (8682522807148012L*181783497276652981L )与系统当前纳秒时间进行异或。

具体实现如下(以下代码为自实现，非java源代码)：

private static final Long multiplier=25214903917l;
	private static final long addend = 11l;
	private static final long mask = (1L << 48) - 1;
	private AtomicLong seed;//保证线程安全
	public MyRandom2(){
		this.seed = new AtomicLong((8682522807148012L*181783497276652981L )^System.nanoTime());
	}

    public int nextInt() {
        return next(32);
    }
    private int next(int bits) {
        long oldseed, nextseed;
        AtomicLong seed = this.seed;
        do {
            oldseed = seed.get();
            nextseed = (oldseed * multiplier + addend) % mask;
        } while (!seed.compareAndSet(oldseed, nextseed));
        return (int)(nextseed >>> (48 - bits));
    }
复制代码

随机化算法应用之素性测试

素性测试介绍

近似确定一个大数是否是素数。 素性测试宣称一个数不是素数，那么可以肯定这个数不是素数，若宣称一个数是素数，那么这个数将以高概率是素数。 素数测试依赖于两个定理，下面介绍。

两个定理

1. 费马小定理 如果一个数P是素数，那么0<A<P,那

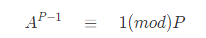
数论中非常著名的定理 例如： 11是素数

该定理为高概率确定一个数是否是素数提供了理论依据，我们只需校验是否

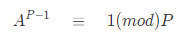
，若不成立P一定不是素数。反之有可能是素数 实验表明，运行50次素数，算法错误的概率为25%。

2. 如果P是素数，0<A<P,那么

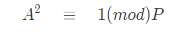
仅有两个解 A=1或者A=P-1。 因此在计算

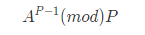
的任意时刻，发现违背该定理，即可确认该数不是素数。

代码

结合两个定理，以随机数生产A，的素性测试代码如下：

package chapter10.random;

import java.util.Random;

/**
 * 一种概率，测试一个数是否是素数
 * 依据
 * 1.费马小定理：如果P是素数，且0<A<P,那么A^(P-1)≡(1 mod P)<br/>
 * 2. 如果P是素数且 0<A<P,那么X^2≡(1 mod P),仅有两个解X=1，P-1<br/>
 * @author Administrator
 */
public class Witness {
    /**
     * A^(P-1)≡(1 mod P)
     * 此处P-1 对应变量n
     */
	private static long witness(long a,long n,long p){
		if(n==0){
			return 1;
		}
		long x=witness(a,n/2,p);
			
		if(x==0){
			return 0;
		}
		//校验定理2
		long y=(x*x)%p;
		if(y==1&&x!=1&&x!=p-1){
			return 0;
		}
		//校验定理2结束
		if(n%2!=0){//奇数,修正A^p-1的解
			y=(a*y)%p;
		}
		return y;
	}


    /**
     * 尝试五次
     */
    public static final int TRIALS = 5;

    /**
     * 素性测试
     */
    public static boolean isPrime( long n ){
        Random r = new Random( );
        for( int counter = 0; counter < TRIALS; counter++ )
            if( witness( r.nextInt( (int) n - 3 ) + 2, n - 1, n ) != 1 )
                return false;

        return true;
    }
    public static void main(String[] args) {
		for(int i=100;i<200;i++){
			if(isPrime(i)){
				//101 103 107 109 113 
				//127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 
				//199
				System.out.println(i);
			}
		}
	}
}

复制代码