转载

著名数学家宣布解决算法难题或破30年僵局

　　文/Erica Klarreich 译/沈庞（微信公众号：赛先生）

　　一个被理论计算机科学家誉为突破性的算法诞生了。这个算法可以映射出当前复杂性理论(complexity theory)的深奥程度，并探索出计算问题(computational problems)究竟该如何解决。也就是上个月，芝加哥大学的数学和计算机科学教授László Babai (编者注：Babai 是今年 Knuth Prize 得主)宣布他想出了一个新的解决“图同构”问题的算法——这个问题在计算机科学中算得上是最诱人的奥秘。Babai 教授认为，他的新算法比以往算法的效率都要高，即使是曾经保持 30 多年记录的最佳算法。他的论文已经提交给美国计算机协会第 48 届计算理论会议，并已能在预印本文库 arxiv.org 上下载。

　　几十年来，图同构问题(graph isomorphism problem)在复杂性理论中享有特殊的地位。相比其他计算问题，人们能很容易把它们分类成难或易，但图同构问题却无法做这样的分类。它似乎比容易的问题更困难，但比困难的问题更容易，就像落入两者间的一块无人之境。它是这块灰色地带里最著名的两个问题之一。麻省理工学院的复杂性理论学家 Scott Aaronson 教授评论说：“现在看来，另一个可能要一枝独秀了”。Babai 教授的工作的确刺激了理论计算机科学家。正如圣菲研究所(Santa Fe Institute.)的计算机科学家 Joshua Grochow 所说：“如果他的研究正确，那么即便不是近几十年，也是近十年中的大成就了。”

　　计算机科学家使用“图”(graph)这个词来指代一种网络，这种网络是由若干给定的点及连接两点的线所构成的。简单来说，图的同构问题是：如何判断两张图是否是同样的图。也就是说，两个图的点是一一对应(即“同构”)，维持相同的节点连接方式。这个问题很容易表述，但很难解决。因为即使是很小的图，只要通过移动节点的位置，就可以使其看起来完全不同。

　　现在，问题的难度水平好像降低了，而 Babai 教授的工作为此作出了重要的一步，即通过他所阐述的“准多项式时间”(quasi-polynomial-time)算法来解决。正如 Aaronson 教授所描述，这个算法把图同构问题放到了P类问题的“大都市圈”内(译者注：P类问题指存在多项式级复杂度算法的问题，见下文)，于是就可以用经典的办法有效地解决它。虽然这项新工作还不至于为困难的图同构问题画上句号，但许多研究者把它视作一种游戏规则的改变。对此，Grochow 评论道：“在他发表之前，我认为除了他自己，任何人都会觉得这个问题无法在未来 10 年内解决，甚至永远解决不了。”

著名数学家宣布解决算法难题或破30年僵局

11 月 10 日，Babai 教授在芝加哥大学宣讲他的图同构算法

　　最近几周，Babai 已经作了 4 次讲座，对学者们陈述他的算法，然而在其他专家对他的新论文审查通过前还尚需时日。所以 Babai 拒绝向媒体发言，他在一封电子邮件中写道：“科学的完整性要求我：新结果必须在对媒体公开前通过同行专家彻底的审查。”

　　其他研究人员倒是谨慎又乐观地认为：他的证明将取得成功。“Babai 有很好的声誉”，Aaronson 教授说，“他是名副其实地值得信赖。”

　　来自加州大学伯克利分校的计算机科学家 Luca Trevisan 也在 Babai 的第二次讲座之后评论说：“我们对此都很乐观。假定证明是正确的，那就是一个标志性的成果。”

　　一项盲测

　　如何对给定的 2 个图检查它们是否同构?一种方法是：简单地去比较每一个点来匹配另一个图中可能对应的所有节点。但一张具有n个节点的图，如此匹配的计算数量就为n的阶乘(1 * 2 * 3 *…* N)，远远超过n的数量级。这种比蛮力的方法非常不切实际，只适用于极少节点的图。假如图里只有 10 个节点，也已经需要 300 多万次可能的匹配检查。对于 100 个节点的图，可能的匹配数大概会远远超过可见宇宙中的原子数。

　　一般计算机科学家们认为，一个算法若能有效率，其运行时间必须是一个多项式而不是阶乘，如n的二次方或三次方;毕竟多项式的增长比起阶乘或指数函数(2 的n次方)来要慢得多。所以能用多项式时间解决的算法问题被统称为P类问题。自这个分类首次在几十年前提出，已经有数千个自然科学和工程领域的问题被证明归于此类。

　　计算机科学家认为，P类问题是相对容易的问题，而另一个类别里的数千个问题则比较难，即“NP 完全”问题(NP-complete)。从来没有人为 NP 完全问题找到过一个有效的算法，大多数计算科学家甚至认为没有人会找到。于是，在数学上，“NP 完全问题是否真的比P类问题更难”则成了价值百万美金的 P vs NP 问题，也被广泛认为是最重要的问题之一。

　　图同构问题既不是已知的P问题，也不是已知的 NP 完全问题。其实，它似乎徘徊在这两者之间。它就好像在自然问题里占据了唯一的小块灰色边缘之境;而唯一和它并肩齐名的问题是素数分解问题(分解质因数)。如 Grochow 所言：“很多人都会花时间在图同构问题上，因为它说起来是一个非常自然的、简单的问题，却又是那么神秘。”

　　本来，人们有充分的理由怀疑图同构是 NP 完全问题。但是，它有一个奇怪的属性，一个其他 NP 完全问题没有的属性：在理论上，它是可能有解的。比如，一个无所不知的人(以下用“梅林”代称)要让一个普通人(以下用“亚瑟”代称)相信，两张图是不同的。即便他没有给出任何差异之处的提示，普通人却也能分辨出来。

　　这种“零知识”证明类似于，梅林要说明可口可乐和百事可乐有不同的配方，而亚瑟不了解它们之间的差异。于是梅林给亚瑟反复地盲测，如果亚瑟能始终正确识别可口可乐和百事可乐的味道，那么他也会接受这两种饮料是不同的。

　　同样，如果梅林告诉亚瑟，2 个图是不同的，亚瑟也就用盲测来验证这个说法。亚瑟把两个图形遮起来，然后移动它们各自的节点，使它们看起来与初始的样子不同。然后再拿给梅林问他，哪一张是哪一张。如果这两者是同构的，梅林就无法回答。但如果梅林一次又一次地能答对这些问题，亚瑟就会得出结论：两张图肯定是不同的，即使他自己不能发现其中的差异。

　　从来没有人发现用一个盲测就能解决任何一个 NP 完全问题。鉴于这个以及其他的原因，理论计算科学家们达成了一个普遍的共识：图同构可能不是 NP 完全问题。

　　而对于反向的问题——图同构是否属于P类问题——的证据则更混杂。一方面，实践中的图同构算法不能有效地解决这个问题。而几乎所有图，你都能找到可行的算法，甚至你能随机选择算法。计算机科学家们不得不努力工作来从中纠错。

　　另一方面，图同构也被计算机科学家称为“普遍级”的问题。任何涉及到两种“组合结构”是否同构的问题都和图同构相关。比如：两张不同的数独游戏，是否是同一道益智问题——这些都可以改写为图同构问题。这意味着如果有一个图同构的快速算法将一次性解决所有这些问题。Grochow 说：“通常当一个问题有这样的普遍性，它也就意味着一种困难”。

　　2012 年，马里兰大学的计算机科学家，William Gasarch 曾对图同构问题有过一次非正式的调查。他发现，在他调查的理论计算机科学家中，有 14 人认为这属于P类问题，而 6 人认为它不是。在 Babai 发表之前，很多人都没想到这个问题能在短期内解决。比如 Grochow 认为它不是P问题，也可能是P问题，总之在有生之年，他都不一定会知道。

　　用数字作图

　　Babai 提出的算法并没有把图同构全部带入P类问题，但它已经很接近了。它被称为准多项式，他断言，这意味着一张有n个节点的图，其算法的运行时间虽然不具有n的恒定增长率(如多项式中的那样)，但可以类比成同样缓慢的增长率。

　　曾经对图同构最好的算法是由 Babai 和 Eugene Luks (如今俄勒冈大学的名誉教授)在 1983 年一起参与创立的。它的运行速度为“次指数”时间。其运行时间与新算法“准多项式”之间的差距，就相当于指数到多项式速度的差距。Babai 教授从 1977 年起一直在图同构问题上工作至今，“他琢磨这个问题大约已经有 40 年”，Aaronson 对此非常了解。

　　Babai 的新算法是以第一张图的一些小节点开始，实际会给它们每一个点“画”上不同的颜色。然后，它假设第二张图里有其一一对应的点，开始在其中寻找同构，并在找到后将这些对应节点标上相同的颜色。该算法循环往复直到最终验证完所有可能的猜测。

　　一旦初始猜测正确的被涂好颜色，那么它就限制了其他节点的连接。例如，在第一张图里有个蓝色节点，那么与其连接的另一个未标注颜色的节点在第二个图里也必须对应于一个与蓝色节点连接的点。为了追踪这些条件，该算法就会引入新的颜色并标注：比如若该点被链接到 1 个蓝色点和 1 个红色点则标为黄色，或者若它有连接到 1 个红色节点 2 个黄色点则标为绿色，等等。该算法会不断引入更多的颜色，直到没有其余的连接特征供其捕捉。

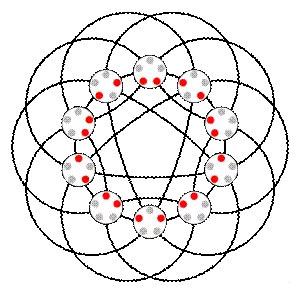
著名数学家宣布解决算法难题或破30年僵局

高度对称的“约翰逊图”是他的算法方案里没有涵盖的唯一案例

　　一旦图变成彩色的，该算法就可以依据节点中不同的颜色去排除所有的匹配。如果算法足够幸运，整个绘画的过程就能将图分成许多不同颜色区块，这就大大减少了一些算法必须考虑的可能同构数目。如果情况相反，大部分节点的颜色相同，那么就采用 Babai 开发的另一种不同方式来减少可能的同构数。除了一种情况作为例外：即两图都包含“约翰逊图式”的相关结构时。因为约翰逊图包含有太多的对称性，使得涂点的过程和 Babai 的进一步改进尚不足以对该算法提供指导。

　　11 月 10 日，在新算法的第一次讲座上，Babai 称这些“约翰逊图”对致力于用涂点方案解决图同构问题的计算机科学家们来说是“无法形容的痛苦之源”。但约翰逊图可以通过其他算法比较容易地处理，所以即便这些图是他涂点方案的唯一障碍，Babai 也能够驯服它们。

　　“他的做法是一个非常符合自然的策略，而且在某种意义上说非常明快”，芝加哥大学的计算机科学家，Janos Simon 评论 Babai 的方案时说，“这很可能是正确的，只是所有数学家都很谨慎。”

　　虽然新的算法已经把图同构问题比以往更拉向P类问题，但 Babai 在他的第一次讲座里猜测，图同构问题可能在P类问题的边界——即在郊区而不是城市中心。Trevisan 说这的确是最有趣的可能性，因为它会使图同构这样的第一自然问题有个拟多项式的算法，但没有多项式的算法。他说：“这就表明，复杂性理论的领域远比我们想象的要丰富得多”。然而，即便此话当真，也不要指望很快就有证据出现：用以证明它将能大量解决P与 NP 的问题。因为，这个算法只意味着把图同构从 NP 完全问题中分离出P类问题。

　　事实上，许多计算机科学家相信，图同构正进入一条推进轨道，最终滑入P类问题。Trevisan 认为，这是常见的趋势，一旦一个拟多项式算法被发现，大家就会这样预测，等待再一次的突破。他说：“总之，这个问题已经带给我们不少惊讶了，但也许还会有更多的惊喜即将到来。”

正文到此结束