SparseArray:解析与实现
介绍
Android提供了SparseArray,这也是一种KV形式的数据结构,提供了类似于Map的功能。但是实现方法却和HashMap不一样。它与Map相比,可以说是各有千秋。
优点
- 占用内存空间小,没有额外的Entry对象
- 没有Auto-Boxing
缺点
- 不支持任意类型的Key,只支持数字类型(int,long)
- 数据条数特别多的时候,效率会低于HashMap,因为它是基于二分查找去找数据的
相关参考 SparseArray vs HashMap
总的来说,SparseArray适用于数据量不是很大,同时Key又是数字类型的场景。
比如,存储某月中每天的某种数据,最多也只有31个,同时它的key也是数字(可以使用1-31,也可以使用时间戳)。
再比如,你想要存储userid与用户数据的映射,就可以使用这个来存储。
接下来,我将讲解它的特性与实现细节。
直观的认知
它使用的是两个数组来存储数据,一个数组存储key,另一个数组来存储value。随着我们不断的增加删除数据,它在内存中是怎么样的呢?我们需要有一个直观的认识,能帮助我们更好的理解和体会它。
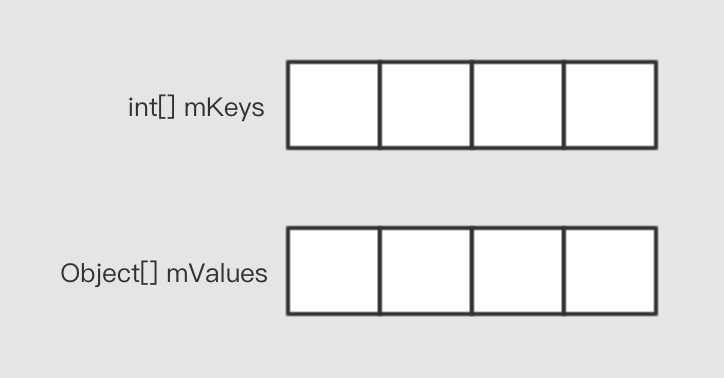
初始化的状态
内部有两个数组变量来存储对应的数据, mKeys 用来存储key, mValues 用来存储泛型数据,注意,这里使用了 Object[] 来存储泛型数据,而不是 T[] 。为什么呢?这个后面在讲。
插入数据
如下图所示,插入数据,总是“紧贴”数组的左侧,换句话说,总是从最左边的一个空位开始使用。我一开始没详细探究的时候,都以为它是类似 HashMap 那样稀疏的存储。
另一个值得注意的事情是,key总是 有序的 ,不管经过多少次插入,key数组中,key总是从小到大排列。

扩容
当一直插入数据,快满的时候,就会自动的扩容,创建一个更大的数组出来,将现有的数据全部复制过去,再插入新的数据。这是基于数组实现的数据结构共同的特性。
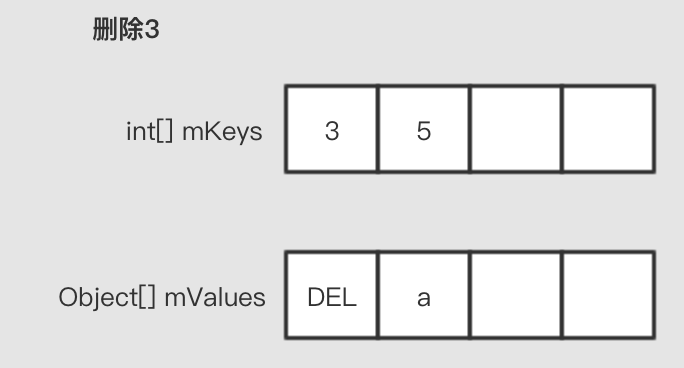
删除
删除是使用标记删除的方法,直接将目标位置的有效元素设置为一个DELETED标记对象。
查询数据
怎么查数据呢?
比如我们查5这个数据 get(5) ,那么它是在 mKeys 中去查找是否存在5,如果存在,返回index,然后用这个index在对应的 mValues 取出对应的值就好了。
实现
接下来我们按照自己的理解,来实现这样的一个数据结构,从而学习它的一些细节和思想,加深对它的理解,有利于在生产中,能更有效的,正确的使用它。
确定接口(API)
首先,确定一下,我们需要暴露什么样的功能给别人使用。当然了,答案是显而易见的,当然是插入,查询,删除等功能了。
public class SparseArray<E> {
public SparseArray() {
}
public SparseArray(int initCap) {
}
public void put(int key, E value) {
}
public E get(int key) {
}
public void delete(int key) {
}
public int size() {
}
}
上面列举了我们需要的功能,无参构造函数,有参数构造函数(期望能主动设置初始容量),put数据,get数据,删除数据,以及获取当前数据有多少。
实现put方法
put数据是最核心的方法,一般我们开发一个东西,也是先开发创建数据的功能,这样才能接着开发展示数据的功能。所以我们先来实现put方法。
按照之前的理解,我们需要一些成员变量来存储数据。
private int[] mKeys; private Object[] mValues; private int mSize = 0;
需要先找到put到什么位置
这里会有两种情况:
- 我要put的key不存在,应该put到什么地方?
- 我要put的key已经存在,直接覆盖
因此第一步,需要先找一下,当前key,是否存在。我们使用二分查找来处理。
public void put(int key, E value) {
int i = BinarySearch.search(mKeys, mSize, key);
if (i >= 0) {
// 找到了有两种情况
// 1.是对应的mValues有一个有效的数据对象,直接覆盖
// 2.对应的mValues里面是一个DELETED对象,同样的,直接覆盖
mValues[i] = value;
} else {
}
}
如果在数组中找到了,那么操作就很简单,直接覆盖就完事了。
如果没找到呢,我们需要将数据插入到正确的位置上,这个所谓正确的位置,指的是,插入之后,依然保证数组有序的情况。打个比方: 1, 4, 5, 8 ,请问 3 应该插入哪里,当然是放到 index=1 的地方,结果就是 1, 3, 4, 5, 8 了。
那如果key不存在,怎么知道应该放到哪里呢?
我们来看一下这个二分查找,它帮我们解决了这个小问题。
public static int search(int[] arr, int size, int target) {
int lo = 0;
int hi = size - 1;
while (lo <= hi) {
final int mid = (lo + hi) >>> 1;
final int value = arr[mid];
if (value == target) {
return mid;
} else if (value > target) {
hi = mid - 1;
} else {
lo = mid + 1;
}
}
return ~lo;
}
按照传统的思想,查找类的API,如果找不到,一般都会返回-1,但是这个二分查找,返回了lo的取反。这会达到什么效果呢。
情况1:数组是空的,那么查找任何东西,都找不到,那会怎么样?根据代码可以知道,循环都进不去,那么直接返回了 ~0 ,也就是最大的负数。我们只需要知道它是一个负数。
情况2:数组不是空的,比如 1, 3, 5 ,我们找 2 ,这里简单的单步执行一下:
lo = 0, size = 3, hi = 2, 好,进入循环 mid = (0 + 2) / 2 = 1, value = 3 value > 2, 所以 hi = 1 - 1 = 0, 再次循环 mid = (0 + 0) / 2 = 0, value = 1 value < 2, so, lo = 0 + 1; 退出循环 返回~1
如果你在尝试去验算其他情况,你会发现,返回值刚好是它应该放置的位置的取反。换句话说,返回值再取反后,就可以得到,这个key应该插入的位置。
这应该是二分查找的一个小技巧。非常的实用!
接下来,想一想,0取反是负数,任何正数取反,也都是负数,也就是说,只要是负数,就代表没找到,再将这个数取反,就得到了,应该put的位置!
所以,代码继续实现为:
public void put(int key, E value) {
int i = BinarySearch.search(mKeys, mSize, key);
if (i >= 0) {
// 找到了有两种情况
// 1.是对应的mValues有一个有效的数据对象,直接覆盖
// 2.对应的mValues里面是一个DELETED对象,同样的,直接覆盖
mValues[i] = value;
} else {
i = ~i;
mKeys = GrowingArrayUtil.insert(mKeys, mSize, i, key);
mValues = GrowingArrayUtil.insert(mValues, mSize, i, value);
mSize++;
}
}
实现get方法
接下来,我们实现get方法。
get方法实现就比较简单了,只需要通过二分查找找到对应的index,再从value数组中取出对象即可。
public E get(int key) {
// 首先查找这个key存不存在
int i = BinarySearch.search(mKeys, mSize, key);
if (i < 0) {
return null;
} else {
return (E)mValues[i];
}
}
实现delete方法
delete方法,就是删除某个key,对应的细节是,找到这个key是否存在,如果存在的话,将value数组中对应位置的数据设置为一个常量 DELETED 。这样做的好处就是比较快捷,而不需要真正的去删除元素。当然由于这个DELETED对象存在value数组中,对put和get以及size方法都会带来一些影响。
下面的代码,定义一个静态的final变量 DELETED 用来作为标记已经删除的变量。
另一个成员变量标记,当前value数组中是否有删除元素这个状态信息。
private static final Object DELETED = new Object();
/**
* 标记是否有DELETED元素标记
* */
private boolean mHasDELETED = false;
public void delete(int key) {
// 删除的时候为标记删除,先要找到是否有这个key,如果没有,就没必要删除了;
// 找到了key看一下对应的value是否已经是DELETED,如果是的话,也没必要再删除了
int i = BinarySearch.search(mKeys, mSize, key);
if (i >= 0 && mValues[i] != DELETED) {
mValues[i] = DELETED;
mHasDELETED = true;
}
}
实现size方法
size方法返回在这个容器中,数据对象有多少个。由于 DELETED 对象的存在,key数组和value数组,以及成员变量 mSize 都没法靠谱得直接得到有效数据的count。
因此这里需要一个内部的工具方法 gc() ,它的作用就是,如果有 DELETED 对象存在,那么就重新整理一下数组,将 DELETED 对象都移除,数组中只保留有效数据即可。
先来看 gc 的实现
private void gc() {
int placeHere = 0;
for (int i = 0; i < mSize; i++) {
Object obj = mValues[i];
if (obj != DELETED) {
if (i != placeHere) {
mKeys[placeHere] = mKeys[i];
mValues[placeHere] = obj;
mValues[i] = null;
}
placeHere++;
}
}
mHasDELETED = false;
mSize = placeHere;
}
它的内部逻辑很简单,就是从头到尾遍历value数组,把每一个不是 DELETED 的对象都重新放置一遍,覆盖掉前面的 DELETED 对象。
然后,我们再看一下size的实现
public int size() {
if (mHasDELETED) {
gc();
}
return mSize;
}
完善get方法
假设有这样的一个场景, put(1, a), put(2, b), delete(2), get(2) 。按照现在的get实现,就会返回 DELETED 对象出去,所以,由于 DELETED 的存在,我们需要完善一下get方法的逻辑。
public E get(int key) {
// 首先查找这个key存不存在
int i = BinarySearch.search(mKeys, mSize, key);
// 这里有两种情况
// 如果key小于0,说明在mKeys中,没有目标key,没找到
// 如果key大于0,还要看一下,对应的mValues中,是否那个元素是DELETED,因为删除的时候是标记删除的
// 以上两种情况都是没有找到
if (i < 0 || mValues[i] == DELETED) {
return null;
} else {
return (E)mValues[i];
}
}
完善put方法
补充的代码上面我都写了注释,讲解了这两坨额外的代码是用来处理什么情况的。
public void put(int key, E value) {
int i = BinarySearch.search(mKeys, mSize, key);
if (i >= 0) {
// 找到了有两种情况
// 1.是对应的mValues有一个有效的数据对象,直接覆盖
// 2.对应的mValues里面是一个DELETED对象,同样的,直接覆盖
mValues[i] = value;
} else {
i = ~i;
// 这一段代码是处理这一的场景的
// 1 2 3 5, delete 5, put 4
if (i < mSize && mValues[i] == DELETED) {
mKeys[i] = key;
mValues[i] = value;
return;
}
// 另一种情况
// 如果有删除的元素,并且数组装满了,这个时候需要先GC,再重新搜一下key的位置
if (mHasDELETED && mSize >= mKeys.length) {
gc();
i = ~BinarySearch.search(mKeys, mSize, key);
}
mKeys = GrowingArrayUtil.insert(mKeys, mSize, i, key);
mValues = GrowingArrayUtil.insert(mValues, mSize, i, value);
mSize++;
}
}
最后,GrowingArrayUtil.insert是做了什么?
其实说起来很简单,用一个过程来概括一下一般情况。
[1, 2, 3, 4, 5, 0, 0, 0, 0, 0] insert(index=2, value=99) 1.复制index=2以前的元素 [1, 2, 3, 4, 5, 0, 0, 0, 0, 0] 2.复制index=2以后的元素,往后挪一位 [1, 2, 3, 3, 4, 5, 0, 0, 0, 0] 3.将index=2的位置,放入99 [1, 2, 99, 3, 4, 5, 0, 0, 0, 0]
当然,这里要处理,如果刚好数据满了,插入新数据,就需要创建一个新的,更大的数组来复制以前的数据了。
/**
* @param rawArr 原始数组
* @param size 有效数据的长度,与数组长度不一样,如果数组长度大于有效数据的长度,那么往里面插入数据是OK的
* 如果有效数据的长度等于数组的长度,那么要插入数据,就要创建更大的数组
* @param insertIndex 插入index
* @param insertValue 插入到index的数值
* */
public static int[] insert(int[] rawArr, int size, int insertIndex, int insertValue) {
if (size < rawArr.length) {
System.arraycopy(rawArr, insertIndex, rawArr, insertIndex + 1, size - insertIndex);
rawArr[insertIndex] = insertValue;
return rawArr;
}
int[] newArr = new int[rawArr.length * 2];
System.arraycopy(rawArr, 0, newArr, 0, insertIndex);
newArr[insertIndex] = insertValue;
System.arraycopy(rawArr, insertIndex, newArr, insertIndex + 1, size - insertIndex);
return newArr;
}
public static <T> Object[] insert(Object[] rawArr, int size, int insertIndex, T insertValue) {
if (size < rawArr.length) {
System.arraycopy(rawArr, insertIndex, rawArr, insertIndex + 1, size - insertIndex);
rawArr[insertIndex] = insertValue;
return rawArr;
}
Object[] newArr = new Object[rawArr.length * 2];
System.arraycopy(rawArr, 0, newArr, 0, insertIndex);
newArr[insertIndex] = insertValue;
System.arraycopy(rawArr, insertIndex, newArr, insertIndex + 1, size - insertIndex);
return newArr;
}
好了,关于 SparseArray 的讲解就到这里结束了。完整的源码可以查看 我写的 ,也可以查看 官方的 。
之前提到的一些疑问点
- 为什么用
Object[],而不是T[]
我的理解是,如果使用泛型数组 T[] ,你就必须构造出一个泛型数组,那么构造泛型数组,你需要能创建泛型对象,也就是说,必须调用 T 的构造函数才能创建泛型对象,但是由于是泛型,构造函数是不确定的,只能通过反射的形式来调用,这样显然就效率和稳定性上有一些问题。因此大多数泛型的实现,都是通过 Object 对象来存储泛型数据。
如果你觉得这篇内容对你有帮助的话,不妨打赏一下,哪怕是小小的一份支持与鼓励,也会给我带来巨大的动力,谢谢:)












![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)

