转载

Swift 算法实战之路：深度和广度优先搜索

之前谈到了最简单的搜索法：二分搜索。虽然它的算法复杂度非常低只有O(logn)，但使用起来也有局限：只有在输入是排序的情况下才能使用。这次讲解两个更复杂的搜索算法 – 深度优先搜索（Depth-First-Search，以下简称DFS）和广度优先搜索（Breadth-First-Search，以下简称BFS）。

基本概念

DFS和BFS的具体定义这里不做赘述。笔者谈谈自己对此的形象理解：假如你在家中发现钥匙不见了，为了找到钥匙，你有两种选择：

从当前角落开始，顺着一个方向不停的找。假如这个方向全部搜索完毕依然没有找到钥匙，就回到起始角落，从另一个方向寻找，直到找到钥匙或所有方向都搜索完毕为止。这种方法就是DFS。从当前角落开始，每次把最近所有方向的角落全部搜索一遍，直到找到钥匙或所有方向都搜索完毕为止。这种方法就是BFS。我们假设共有10个角落，起始角落为1，它的周围有4个方向，如下图：

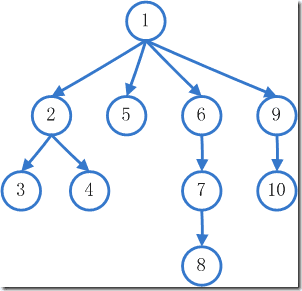
Swift 算法实战之路：深度和广度优先搜索

DFS的搜索步骤

2 -> 3 -> 4
6 ->7 -> 8
9 -> 10

即每次把一个方向彻底搜索完全后，才返回搜索下一个方向。

BFS的搜索步骤

2 -> 5 -> 6 -> 9
3 -> 4
10

即每次访问上一步周围所有方向上的角落。细心的朋友会记得，我之前在讲二叉树的时候，讲到了前序遍历和层级遍历，而这两者本质上就是DFS和BFS。

DFS的Swift实现

 
funcdfs(root: Node?) {
    guardletroot = rootelse {
        return
    }
 
    visit(root)
    root.visited = true
 
    fornodein root.neighbors {
        if !node.visited {
            dfs(node)
        }
    }
}

BFS的Swift实现

 
funcbfs(root: Node?) {
    varqueue = [Node]()
 
    if letroot = root {
        queue.append(root)
    }
 
    while !queue.isEmpty {
        letcurrent = queue.removeFirst()
 
        visit(current)
        current.visited = true
 
        fornodein current.neighbors {
            if !node.visited {
                queue.append(node)
            }
        }
    }
}

永远记住：DFS的实现用递归，BFS的实现用循环（配合队列）。

iOS实战演练

硅谷面试iOS工程师，有这样一个环节，给你1 ~ 1.5小时，从头开始实现一个小App。我们来看这样一个题目：

实现一个找单词App: 给定一个初始的字母矩阵，你可以从任一字母开始，上下左右，任意方向、任意长度，选出其中所有单词。

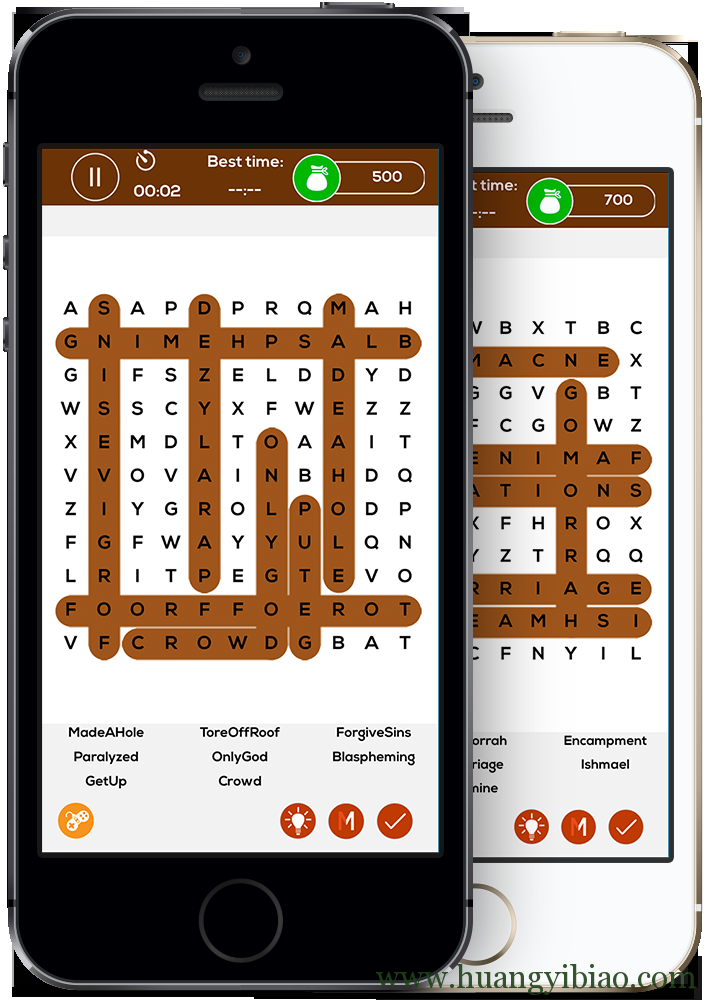
Swift 算法实战之路：深度和广度优先搜索

很多人拿到这道题目就懵了。。。完全不是我们熟悉的UITableView或者UICollectionView啊，这要咋整。我们来一步步分析。

第一步：实现字母矩阵

首先，我们肯定有个字符二阶矩阵作为输入，姑且记做：let matrix: [[Character]]。现在要把它展现在手机上，其实很简单，就是写一个UILabel，其行数是matrix的行数，然后把matrix的每一行作为一个字符串打印在UILabel上即可。

第二步：用DFS实现搜索单词

现在要实现搜索单词的核心算法了。我们先简化要求，假如只在字母矩阵中搜索单词 crowd 该怎么做？首先我们要找到 c 这个字母所在的位置，然后再上下左右找第二个字母 r ，接着再找字母 o 。。。以此类推，直到找到最后一个字母 d 。如果没有找到相应的字母，我们就回头去首字母 c 所在的另一个位置，重新搜索。这里要注意一个细节，就是我们不能回头搜索字母。比如我们已经从 c 开始向上走搜索到了 r ，这个时候就不能从 r 向下回头 – 因为 c 已经访问过了。所以这里需要一个var visited: [[Bool]] 来记录访问记录。代码如下：

 
funcsearchWord(board: [[Character]]) -> Bool {
    guardboard.count > 0 && board[0].count > 0 else {
        return false
    }
 
    let m = board.count
    let n = board[0].count
    varvisited = Array(count: m,repeatedValue: Array(count: n,repeatedValue: false))
    varwordContent = [Character]("crowd".characters)
 
    for i in 0 ..< m {
        for j in 0 ..< n {
            if board[i][j] == wordContent[0] && dfs(board, wordContent, m, n, i, j, &visited, 0) {
                return true
            }
        }
    }
 
    return false
}
 
funcdfs(board: [[Character]], _wordContent: [Character], _m: Int, _n: Int, _i: Int, _j: Int, inout _visited: [[Bool]], _index: Int) -> Bool {
    if index == wordContent.count {
        return true
    }
 
    guard i >= 0 && i < m && j >= 0 && j < n else {
        return false
    }
    guard !visited[i][j] && board[i][j] == wordContent[index]else {
        return false
    }
 
    visited[i][j] = true
 
    if dfs(board, wordContent, m, n, i + 1, j, &visited, index + 1) || dfs(board, wordContent, m, n, i - 1, j, &visited, index + 1) || dfs(board, wordContent, m, n, i, j + 1, &visited, index + 1) || dfs(board, wordContent, m, n, i, j - 1, &visited, index + 1) {
        return true
    }
    visited[i][j] = false
 
    return false
}

第三步：优化算法，进阶

好了现在我们已经知道了怎么搜索一个单词了，那么多个单词怎么搜索？首先题目是要求找出所有的单词，那么肯定事先有个字典，根据这个字典，我们可以知道所选字母是不是可以构成一个单词。所以题目就变成了：

已知一个字母构成的二维矩阵，并给定一个字典。选出二维矩阵中所有横向或者纵向的单词。

也就是实现以下函数：

 
funcfindWords(board: [[Character]], _dict: Set<String>) -> [String] {}

我们刚才已经知道如何在矩阵中搜索一个单词了。所以最暴力的做法，就是在矩阵中，搜索所有字典中的单词，如果存在就添加在输出中。这个做法显然复杂度极高：因为首先，每次DFS的复杂度就是O(n

2)，字母矩阵越大，搜索时间就越长；其次，字典可能会非常大，如果每个单词都搜索一遍，开销太大。这种做法的总复杂度为O(m·n

2)，其中m为字典中单词的数量，n为矩阵的边长。

这个时候就要引入Trie树（前缀树）。首先我们把字典转化为前缀树，这样的好处在于它可以检测矩阵中字母构成的前缀是不是一个单词的前缀，如果不是就没必要继续DFS下去了。这样我们就把搜索字典中的每一个单词，转化为了只搜字母矩阵。代码如下：

 
funcfindWords(board: [[Character]], _dict: Set<String>) -> [String] {
  varres = [String]()
 
  let m = board.count
  let n = board[0].count
 
  lettrie = _convertSetToTrie(dict)
  varvisited = Array(count: m,repeatedValue: Array(count: n,repeatedValue: false))
 
  for i in 0 ..< m {
    for j in 0 ..< n {
      _dfs(board, m, n, i, j, &visited, &res, trie, "")
    }
  }
 
  return res
}
 
privatefunc_dfs(board: [[Character]], _m: Int, _n: Int, _i: Int, _j: Int, inout _visited: [[Bool]], inout _res: [String], _trie: Trie, _str: String) {
  // 越界
  guard i >= 0 && i < m && j >= 0 && j < n else {
    return
  }
 
  // 已经访问过了
  guard !visited[i][j]else {
    return
  }
 
  // 搜索目前字母组合是否是单词前缀
  varstr = str + "/(board[i][j])"
  guardtrie.prefixWith(str) else {
    return
  }
 
  // 确认当前字母组合是否为单词
  if trie.isWord(str) && !res.contains(str) {
    res.append(str)
  }
 
  // 继续搜索上下左右四个方向
  visited[i][j] = true
  _dfs(board, m, n, i + 1, j, &visited, &res, trie, str)
  _dfs(board, m, n, i - 1, j, &visited, &res, trie, str)
  _dfs(board, m, n, i, j + 1, &visited, &res, trie, str)
  _dfs(board, m, n, i, j - 1, &visited, &res, trie, str)
  visited[i][j] = true
}

这里对Trie不做深入展开，有兴趣的朋友自行搜索。